Công thức tỷ giá kỳ hạn | Định nghĩa và tính toán (với các ví dụ)
Công thức tính tỷ giá kỳ hạn
Công thức tỷ giá kỳ hạn giúp giải mã đường cong lợi tức là một biểu diễn đồ họa của lợi suất trên các trái phiếu khác nhau có thời gian đáo hạn khác nhau. Nó có thể được tính toán dựa trên tỷ giá giao ngay vào ngày tương lai xa hơn và một ngày tương lai gần hơn và số năm cho đến ngày tương lai xa hơn và ngày tương lai gần hơn.
Tỷ lệ chuyển tiếp = [(1 + S 1 ) n 1 / (1 + S 2 ) n 2 ] 1 / (n 1 -n 2 ) - 1trong đó S 1 = Tỷ giá giao ngay cho đến một ngày trong tương lai xa hơn,
- S 2 = Tỷ giá giao ngay cho đến một ngày gần hơn trong tương lai, n 1 = Số năm cho đến một ngày trong tương lai xa hơn,
- n 2 = Số năm cho đến một ngày trong tương lai gần hơn
Kí hiệu cho công thức thường được biểu diễn là F (2,1) có nghĩa là lãi suất một năm hai năm kể từ bây giờ.
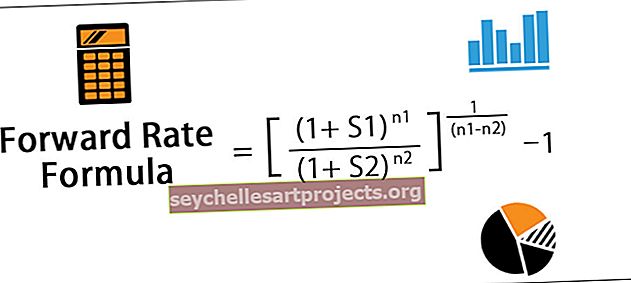
Tính toán tỷ giá kỳ hạn (Từng bước)
Nó có thể được rút ra bằng cách sử dụng các bước sau:
- Bước 1: Đầu tiên, xác định tỷ giá giao ngay cho đến ngày tương lai để mua hoặc bán chứng khoán và nó được ký hiệu là S 1 . Ngoài ra, tính toán số không. của năm cho đến ngày trong tương lai xa hơn và nó được ký hiệu là n 1 .
- Bước 2: Tiếp theo, xác định tỷ giá giao ngay cho đến ngày gần nhất trong tương lai để bán hoặc mua cùng một chứng khoán và nó được ký hiệu là S 2 . Sau đó, tính toán số không. của năm cho đến ngày tương lai gần hơn và nó được ký hiệu là n 2 .
- Bước 3: Cuối cùng, tính toán tỷ giá kỳ hạn cho (n 1 - n 2 ) không. năm sau n 2 không. của năm được hiển thị bên dưới. Tỷ giá chuyển tiếp = [(1 + S 1 ) n 1 / (1 + S 2 ) n 2 ] 1 / (n 1 -n 2 ) - 1
Các ví dụ
Bạn có thể tải xuống Mẫu Excel Công thức Tỷ giá Chuyển tiếp này tại đây - Mẫu Excel Công thức Tỷ giá Chuyển tiếpVí dụ 1
Chúng ta hãy lấy ví dụ về một công ty PQR Ltd đã phát hành trái phiếu gần đây để huy động tiền cho dự án sắp hoàn thành trong hai năm tới. Trái phiếu phát hành có kỳ hạn một năm cung cấp 6,5% lợi tức đầu tư, trong khi trái phiếu có kỳ hạn hai năm cung cấp 7,5% như lợi tức đầu tư. Dựa trên dữ liệu đã cho, hãy tính lãi suất một năm một năm kể từ bây giờ.
Được,
- Tỷ giá giao ngay trong hai năm, S 1 = 7,5%
- Tỷ giá giao ngay trong một năm, S 2 = 6,5%
- Số năm đối với trái phiếu thứ 2, n 1 = 2 năm
- Số năm đối với trái phiếu thứ nhất, n 2 = 1 năm

Theo dữ liệu đưa ra ở trên, chúng tôi sẽ tính lãi suất một năm kể từ bây giờ của công ty POR ltd.
Do đó, việc tính toán tỷ giá kỳ hạn một năm sau một năm kể từ bây giờ sẽ là,

F (1,1) = [(1 + S 1 ) n 1 / (1 + S 2 ) n 2 ] 1 / (n 1 -n 2 ) -
= [(1 + 7,5%) 2 / (1 + 6,5%) 1] 1 / (2-1) - 1

FR một năm một năm kể từ bây giờ = 8,51%
Ví dụ số 2
Chúng ta hãy lấy ví dụ về một công ty môi giới đã hoạt động trong hơn một thập kỷ. Công ty đã cung cấp thông tin sau đây. Bảng này cung cấp một ảnh chụp nhanh về tính toán chi tiết của tỷ giá kỳ hạn.
- Tỷ giá giao ngay trong một năm, S 1 = 5,00%
- F (1,1) = 6,50%
- F (1,2) = 6,00%
Dựa trên dữ liệu đã cho, hãy tính tỷ giá giao ngay trong hai năm và ba năm. Sau đó, hãy tính lãi suất kỳ hạn một năm sau hai năm kể từ bây giờ.
- Cho trước, S 1 = 5,00%
- F (1,1) = 6,50%
- F (1,2) = 6,00%

Do đó, tỷ giá giao ngay trong hai năm có thể được tính là,
S 2 = [(1 + S 1 ) * (1 + F (1,1))] 1/2 - 1
= [(1 + 5,00%) * (1 + 6,50%)] 1/2 -

Tỷ giá giao ngay trong hai năm = 5,75%
Do đó, tính toán tỷ giá giao ngay trong ba năm sẽ là,
S 3 = [(1 + S 1 ) * (1 + F (1,2)) 2] 1/3 -
= [(1 + 5,00%) * (1 + 6,00%) 2] 1/3 -

Tỷ giá giao ngay trong ba năm = 5,67%
Do đó, việc tính toán tỷ giá kỳ hạn một năm trong hai năm kể từ bây giờ sẽ là,

F (2,1) = [(1 + S 3 ) 3 / (1 + S 2 ) 2] 1 / (3-2) -
= [(1 + 5,67%) 3 / (1 + 5,75%) 2] -

Mức độ liên quan và sử dụng
Tỷ giá kỳ hạn đề cập đến tỷ giá được sử dụng để chiết khấu một khoản thanh toán từ một ngày trong tương lai xa đến một ngày trong tương lai gần hơn. Nó cũng có thể được coi là mối quan hệ bắc cầu giữa hai tỷ giá giao ngay trong tương lai, tức là tỷ giá giao ngay xa hơn và tỷ giá giao ngay gần hơn. Đây là một đánh giá về những gì thị trường tin rằng sẽ là lãi suất trong tương lai đối với các kỳ hạn khác nhau.
Ví dụ, chúng ta hãy giả sử rằng Jack đã nhận được tiền hôm nay và anh ấy muốn tiết kiệm tiền để mua bất động sản một năm kể từ hôm nay. Giờ đây, anh ta có thể đầu tư tiền vào chứng khoán chính phủ để giữ nó an toàn và có tính thanh khoản trong năm tới. Tuy nhiên, trong trường hợp đó, Jack có hai sự lựa chọn: Anh ta có thể mua một trái phiếu chính phủ sẽ đáo hạn trong một năm, hoặc anh ta có thể chọn mua một trái phiếu chính phủ khác sẽ đáo hạn trong sáu tháng và sau đó chuyển tiền trong sáu tháng nữa. - trái phiếu chính phủ tháng khi trái phiếu đầu tiên đáo hạn.
Trong trường hợp cả hai tùy chọn đều tạo ra lợi tức đầu tư như nhau, thì Jack sẽ không quan tâm và chọn một trong hai tùy chọn. Nhưng điều gì sẽ xảy ra nếu lãi suất được cung cấp cho trái phiếu sáu tháng cao hơn trái phiếu một năm. Trong trường hợp đó, anh ta sẽ kiếm được nhiều tiền hơn bằng cách mua trái phiếu sáu tháng ngay bây giờ và chuyển nó sang sáu tháng nữa. Bây giờ, nó có hiệu lực để tính toán lợi nhuận của trái phiếu sáu tháng sáu tháng kể từ bây giờ. Bằng cách này, nó có thể giúp Jack tận dụng lợi nhuận của sự thay đổi theo thời gian như vậy.