seychellesartprojects.org

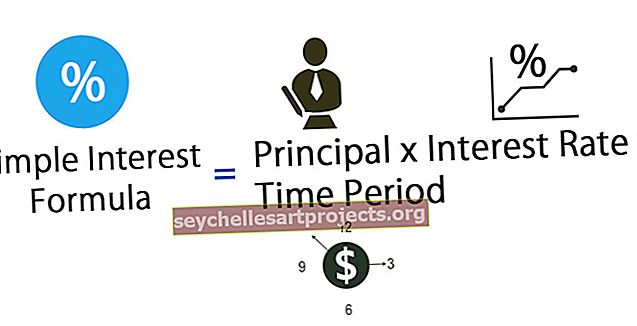
Công thức tính lãi đơn giản (SI)

Lãi suất đơn giản (SI) là một cách tính số tiền lãi phải trả trên tiền gốc và được tính theo một công thức dễ hiểu, đó là nhân số tiền gốc với tỷ lệ lãi suất và số kỳ mà lãi phải trả.

Ở đây, lãi suất chỉ được tính trên số tiền đầu tư ban đầu và không có lãi suất tính theo trường hợp với công thức lãi kép. Nó được sử dụng trong các khoản vay mua ô tô và các khoản vay tiêu dùng khác của các ngân hàng và tổ chức tài chính. Ngoài ra, lãi suất tiền gửi tiết kiệm và tiền gửi có kỳ hạn của ngân hàng cũng được tính theo lãi suất đơn giản.

Các ví dụ

Bạn có thể tải xuống Mẫu Excel Công thức Sở thích Đơn giản này tại đây - Mẫu Excel Công thức Sở thích Đơn giản

Ví dụ 1

ABC cho vay số tiền $ 5000 với mức 10% mỗi năm trong thời hạn 5 năm. Tính tiền lãi đơn giản và tổng số tiền phải trả sau 5 năm.

Tiền gốc: $ 5000

Lãi suất: 10% mỗi năm

Khoảng thời gian (tính bằng năm) = 5

Vì vậy, bây giờ chúng ta sẽ thực hiện phép tính này bằng cách sử dụng phương trình lãi suất đơn giản, tức là

• Tiền lãi đơn giản = Tiền gốc * Lãi suất * Khoảng thời gian
• Lãi suất đơn giản = $ 5000 * 10% * 5
• = $ 2500

Tổng tiền lãi đơn giản trong 5 năm = $ 2500

Số tiền đến hạn sau 5 năm = Tiền gốc + Tiền lãi đơn

• = $ 5000 + $ 2500
• Số tiền đến hạn sau 5 năm = $ 7500.

Ví dụ số 2

Ravi đã mua một chiếc lò vi sóng từ một cửa hàng điện tử có giá 10000 Rs. Anh ấy đã tài trợ khoản tiền tương tự từ ngân hàng HDFC cho vay của nó. Chi tiết như sau:

số tiền cho vay: 12000 Rs

thời gian vay: 1 năm

lãi suất: 10% mỗi năm

Tần suất thanh toán: hàng tháng

Chúng ta có thể tính toán số tiền tương đương hàng tháng trong excel bằng cách sử dụng hàm PMT.

Theo đó, số tiền EMI mà Ravi sẽ phải trả là 879,16 yên (bao gồm cả tiền lãi và tiền gốc). Chúng ta có thể quan sát một cách đơn giản từ biểu phân bổ nợ vay thế chấp dưới đây rằng số tiền lãi tiếp tục giảm theo mỗi lần thanh toán và số tiền gốc tiếp tục tăng; tuy nhiên, khoản trả góp hàng tháng vẫn giữ nguyên trong suốt thời hạn của khoản vay.

Những điểm quan trọng cần lưu ý khi tính lãi đơn giản:

• Khoảng thời gian phải tính bằng năm. Trong trường hợp cùng một tháng, nó nên được chuyển đổi thành năm dưới dạng một phần nhỏ.
• Lãi suất phải được thể hiện trên cơ sở hàng năm, nhưng nếu khoảng thời gian dưới một năm thì nó phải được điều chỉnh trong một năm. Ví dụ, nếu lãi suất là 12% mỗi năm, nhưng vấn đề liên quan đến lãi suất hàng tháng thì nó sẽ là 1% (12% / 12).

Ví dụ # 3

Ram đã vay một khoản vay mua ô tô trị giá 500000 đô la từ Ngân hàng HDBC với lãi suất phải trả là 10% trong thời hạn 24 tháng. Khoản vay sẽ được hoàn trả bằng cách thanh toán bằng nhau hàng tháng là $ 23072,46 (được tính bằng cách sử dụng hàm PMT trong Excel)

Lịch thanh toán được tính bằng công thức SI trong excel như sau:

Chúng ta hãy hiểu khái niệm về công thức SI trong excel bằng cách sử dụng thêm một ví dụ ngành liên quan đến Chứng chỉ tiền gửi (CD).

Ví dụ # 4

Ngân hàng ABC đã đăng ký giấy chứng nhận tiền gửi có tổng trị giá 20000 đô la do chính phủ Ấn Độ cấp với lãi suất 5% mỗi năm. Chứng chỉ tiền gửi sẽ đáo hạn sau 6 tháng.

Tiền lãi mà Ngân hàng ABC thu được trên chứng chỉ tiền gửi:

Tiền lãi đơn giản = Tiền gốc * Lãi suất * Khoảng thời gian

Như vậy Ngân hàng ABC sẽ kiếm được tổng số tiền lãi là $ 500 trên các chứng chỉ tiền gửi khi đáo hạn, tức là sau 6 tháng.

Máy tính lãi đơn giản

Bạn có thể sử dụng Công cụ tính lãi đơn giản sau đây.

Hiệu trưởng
Lãi suất
Khoảng thời gian
Công thức lãi suất đơn giản =

Công thức lãi suất đơn giản =	Tiền gốc x Lãi suất x Khoảng thời gian
	0 x 0 x 0 =	0

Mức độ liên quan và sử dụng

• Lãi suất đơn giản tìm thấy sự liên quan của nó trong cách các Ngân hàng tính lãi trên tài khoản tiết kiệm ngân hàng và các khoản tiền gửi có kỳ hạn do người gửi tiền nắm giữ. Các ngân hàng thường tính lãi hàng quý đối với tiền gửi tiết kiệm và tiền gửi có kỳ hạn.
• Lợi nhuận được tính theo lãi suất đơn giản sẽ luôn nhỏ hơn lợi nhuận được tính theo lãi suất kép vì nó bỏ qua khái niệm lãi kép.
• Công thức SI đảm bảo rằng phần lãi sẽ cao hơn trong các Năm đầu tiên và sau đó sẽ giảm dần khi thời hạn của khoản vay tiến triển.
• Nó được sử dụng để tính lãi cho các khoản vay ngắn hạn như cho vay mua ô tô, chứng chỉ tiền gửi và tài khoản tiết kiệm và tiền gửi có kỳ hạn.