seychellesartprojects.org

Định nghĩa phương pháp hồi quy bình phương nhỏ nhất

Phương pháp hồi quy bình phương nhỏ nhất là một dạng phân tích hồi quy thiết lập mối quan hệ giữa biến phụ thuộc và biến độc lập cùng với một đường tuyến tính. Dòng này được gọi là “dòng phù hợp nhất”.

Phân tích hồi quy là một phương pháp thống kê với sự trợ giúp của nó mà người ta có thể ước tính hoặc dự đoán các giá trị chưa biết của một biến từ các giá trị đã biết của một biến khác. Biến được sử dụng để dự đoán lãi suất thay đổi được gọi là biến độc lập hoặc biến giải thích và biến đang được dự đoán được gọi là biến phụ thuộc hoặc biến giải thích.

Chúng ta hãy xem xét hai biến x & y. Chúng được vẽ trên đồ thị với các giá trị của x trên trục x Các giá trị của y trên trục y. Các giá trị này được biểu thị bằng các dấu chấm trong biểu đồ bên dưới. Một đường thẳng được vẽ qua các dấu chấm - được gọi là đường phù hợp nhất.

Mục tiêu của hồi quy bình phương nhỏ nhất là để đảm bảo rằng đường thẳng được vẽ qua tập hợp các giá trị được cung cấp thiết lập mối quan hệ gần nhất giữa các giá trị.

Công thức hồi quy bình phương nhỏ nhất

Dòng hồi quy theo phương pháp Bình phương nhỏ nhất được tính theo công thức sau:

ŷ = a + bx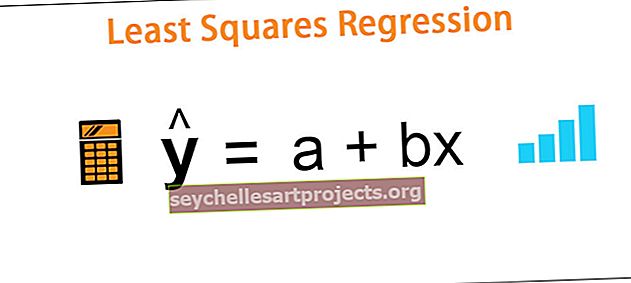

Ở đâu,

• ŷ = biến phụ thuộc
• x = biến độc lập
• a = chặn y
• b = độ dốc của đường

Độ dốc của đường b được tính theo công thức sau:

Hoặc là

Y-intercept, 'a' được tính theo công thức sau:

Dòng phù hợp nhất trong hồi quy hình vuông nhỏ nhất

Đường phù hợp nhất là đường thẳng được vẽ qua một tập hợp các điểm dữ liệu thể hiện tốt nhất mối quan hệ giữa chúng.

Chúng ta hãy xem xét đồ thị sau đây, trong đó một tập dữ liệu được vẽ dọc theo trục x và y. Các điểm dữ liệu này được biểu diễn bằng cách sử dụng các chấm màu xanh lam. Ba đường thẳng được vẽ qua những điểm này - một đường màu xanh lá cây, màu đỏ và màu xanh lam. Đường màu xanh lá cây đi qua một điểm duy nhất và đường màu đỏ đi qua ba điểm dữ liệu. Tuy nhiên, đường màu xanh lam đi qua bốn điểm dữ liệu và khoảng cách giữa các điểm còn lại đến đường màu xanh lam là nhỏ nhất so với hai đường còn lại.

Trong biểu đồ trên, đường màu xanh lam đại diện cho đường phù hợp nhất vì nó nằm gần nhất với tất cả các giá trị và khoảng cách giữa các điểm bên ngoài đường tới đường là nhỏ nhất (nghĩa là khoảng cách giữa phần dư đến đường phù hợp nhất - còn được gọi là tổng bình phương các phần dư). Trong hai đường còn lại, màu cam và màu xanh lá cây, khoảng cách giữa các phần dư đến các đường thẳng lớn hơn so với đường màu xanh lam.

Phương pháp bình phương nhỏ nhất cung cấp mối quan hệ gần nhất giữa các biến phụ thuộc và độc lập bằng cách giảm thiểu khoảng cách giữa các phần dư và dòng phù hợp nhất tức là tổng các bình phương của các phần dư là nhỏ nhất theo cách tiếp cận này. Do đó thuật ngữ "bình phương nhỏ nhất".

Ví dụ về đường hồi quy bình phương nhỏ nhất

Hãy để chúng tôi áp dụng các công thức này trong câu hỏi dưới đây -

Bạn có thể tải xuống Mẫu Excel Hồi quy Bình phương Ít nhất này tại đây - Mẫu Excel Hồi quy Bình phương Ít nhất

Ví dụ 1

Các chi tiết liên quan đến kinh nghiệm của các kỹ thuật viên trong một công ty (trong một số năm) và xếp hạng hiệu suất của họ được cung cấp trong bảng dưới đây. Sử dụng các giá trị này, ước tính xếp hạng hiệu suất cho kỹ thuật viên có 20 năm kinh nghiệm.

Giải pháp -

Để tính toán bình phương nhỏ nhất trước tiên chúng ta sẽ tính giao điểm Y (a) và hệ số góc của đường (b) như sau:

Độ dốc của Đường (b)

• b = 6727 - [(80 * 648) / 8] / 1018 - [(80) 2/8]
• = 247/218
• = 1,13

Y-intercept (a)

• a = 648 - (1,13) (80) / 8
• = 69,7

Đường hồi quy được tính như sau:

Thay 20 cho giá trị của x trong công thức,

• ŷ = a + bx
• ŷ = 69,7 + (1,13) (20)
• ŷ = 92,3

Đánh giá hiệu suất cho một kỹ thuật viên có 20 năm kinh nghiệm được ước tính là 92,3.

Ví dụ số 2

Phương trình hồi quy bình phương nhỏ nhất sử dụng Excel

Phương trình hồi quy bình phương nhỏ nhất có thể được tính bằng excel theo các bước sau:

• Chèn bảng dữ liệu trong excel.

• Chèn biểu đồ phân tán bằng cách sử dụng các điểm dữ liệu.

• Chèn một đường xu hướng trong biểu đồ phân tán.

• Dưới tùy chọn đường xu hướng - chọn đường xu hướng tuyến tính và chọn phương trình hiển thị trên biểu đồ.

• Phương trình hồi quy bình phương nhỏ nhất cho tập dữ liệu excel nhất định được hiển thị trên biểu đồ.

Do đó, phương trình hồi quy bình phương nhỏ nhất cho tập dữ liệu excel đã cho được tính. Sử dụng phương trình, các dự đoán và phân tích xu hướng có thể được thực hiện. Các công cụ Excel cũng cung cấp các tính toán hồi quy chi tiết.

Ưu điểm

• Phương pháp phân tích hồi quy bình phương nhỏ nhất phù hợp nhất cho các mô hình dự đoán và phân tích xu hướng. Nó được sử dụng tốt nhất trong các lĩnh vực kinh tế, tài chính và thị trường chứng khoán, trong đó giá trị của bất kỳ biến nào trong tương lai được dự đoán với sự trợ giúp của các biến hiện có và mối quan hệ giữa các biến tương tự.
• Phương pháp bình phương nhỏ nhất cung cấp mối quan hệ gần nhất giữa các biến. Sự khác biệt giữa tổng bình phương của phần dư với dòng phù hợp nhất là nhỏ nhất theo phương pháp này.
• Cơ chế tính toán đơn giản và dễ áp ​​dụng.

Nhược điểm

• Phương pháp bình phương nhỏ nhất dựa vào việc thiết lập mối quan hệ gần nhất giữa một tập hợp các biến nhất định. Cơ chế tính toán nhạy cảm với dữ liệu và trong trường hợp có bất kỳ ngoại lệ nào (dữ liệu ngoại lệ), kết quả có thể có xu hướng ảnh hưởng lớn.
• Loại tính toán này phù hợp nhất cho mô hình tuyến tính. Đối với các phương trình phi tuyến, các cơ chế tính toán đầy đủ hơn được áp dụng.

Phần kết luận

Phương pháp bình phương nhỏ nhất là một trong những phương pháp được sử dụng phổ biến nhất cho các mô hình dự đoán và phân tích xu hướng. Khi được tính toán phù hợp, nó mang lại kết quả tốt nhất.