Công thức kiểm tra Z trong thống kê | Tính toán từng bước (Ví dụ)

Công thức tính kiểm tra Z trong thống kê

Kiểm định Z trong thống kê đề cập đến kiểm định giả thuyết được sử dụng để xác định xem hai mẫu được tính có khác nhau hay không, trong trường hợp có độ lệch chuẩn và mẫu lớn.

Z = (x - μ) / ơ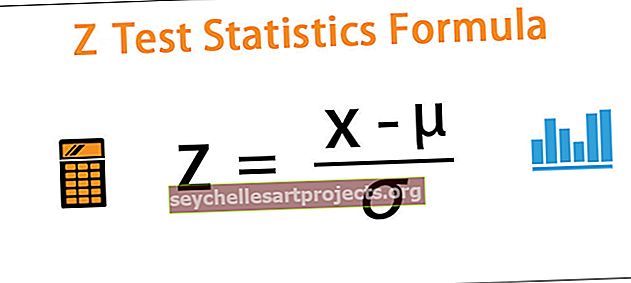

trong đó x = bất kỳ giá trị nào từ tổng thể

μ = dân số trung bình
ơ = độ lệch chuẩn dân số

Trong trường hợp là một mẫu, công thức thống kê z-test về giá trị được tính bằng cách trừ giá trị trung bình của mẫu khỏi giá trị x và sau đó kết quả được chia cho độ lệch chuẩn của mẫu. Về mặt toán học, nó được biểu diễn dưới dạng,

Z = (x - x_mean ) / s

Ở đâu

x = bất kỳ giá trị nào từ mẫu
x_mean = trung bình mẫu
s = độ lệch chuẩn mẫu

Tính toán kiểm tra Z (Từng bước)

Công thức cho thống kê kiểm tra z cho một tập hợp được suy ra bằng cách sử dụng các bước sau:

Bước 1: Trước hết, tính giá trị trung bình dân số và độ lệch chuẩn dân số dựa trên quan sát được thu thập trong trung bình dân số, và mỗi quan sát được ký hiệu là x _i . Tổng số quan sát trong quần thể được ký hiệu là N.

Dân số trung bình,

Độ lệch tiêu chuẩn dân số,

Bước 2: Cuối cùng, thống kê kiểm định z được tính bằng cách trừ trung bình dân số khỏi biến và sau đó kết quả được chia cho độ lệch chuẩn của tổng thể như hình dưới đây.

Z = (x - μ) / ơ

Công thức cho thống kê kiểm tra z cho một mẫu được suy ra bằng cách sử dụng các bước sau:

Bước 1: Đầu tiên, tính giá trị trung bình của mẫu và độ lệch chuẩn của mẫu tương tự như trên. Ở đây, tổng số quan sát trong mẫu được ký hiệu là n sao cho n <N.

Mẫu có nghĩa là,

Độ lệch chuẩn mẫu,

Bước 2: Cuối cùng, thống kê kiểm định z được tính bằng cách trừ giá trị trung bình của mẫu khỏi giá trị x và sau đó kết quả được chia cho độ lệch chuẩn mẫu như hình dưới đây.

Z = (x - x_mean ) / s

Các ví dụ

Bạn có thể tải xuống Mẫu Excel Công thức Kiểm tra Z này tại đây - Mẫu Excel Công thức Kiểm tra Z

Ví dụ 1

Chúng ta hãy giả sử một nhóm học sinh trong một trường học đã xuất hiện trong một bài kiểm tra trong lớp. Điểm trung bình trong bài kiểm tra là 75 và độ lệch chuẩn là 15. Xác định điểm kiểm tra z của David, người đã đạt 90 điểm trong bài kiểm tra.

Được,

Dân số trung bình, μ = 75
Độ lệch chuẩn dân số, ơ = 15

Do đó, thống kê kiểm tra z có thể được tính toán như sau:

Z = (90 - 75) / 15

Thống kê kiểm tra Z sẽ là -

Z = 1

Do đó, điểm kiểm tra của David cao hơn một độ lệch chuẩn so với điểm trung bình của dân số, tức là theo bảng điểm z, 84,13% học sinh đạt điểm thấp hơn David.

Ví dụ số 2

Chúng ta hãy lấy ví dụ về 30 học sinh được chọn làm thành viên của một nhóm mẫu được khảo sát để xem có bao nhiêu chiếc bút chì được sử dụng trong một tuần. Xác định điểm của bài kiểm tra z cho học sinh thứ 3 dựa trên các câu trả lời đã cho: 3, 2, 5, 6, 4, 7, 4, 3, 3, 8, 3, 1, 3, 6, 5, 2, 4 , 3, 6, 4, 5, 2, 2, 4, 4, 2, 8, 3, 6, 7.

Được,

x = 5, vì phản ứng của học sinh thứ 3 là 5
Cỡ mẫu, n = 30

Trung bình mẫu, = (3 + 2 + 5 + 6 + 4 + 7 + 4 + 3 + 3 + 8 + 3 + 1 + 3 + 6 + 5 + 2 + 4 + 3 + 6 + 4 + 5 + 2 + 2 + 4 + 4 + 2 + 8 + 3 + 6 + 7) / 30

Trung bình = 4,17

Bây giờ, độ lệch chuẩn mẫu có thể được tính bằng cách sử dụng công thức trên.

ơ = 1,90

Do đó, điểm z-test của học sinh thứ 3 có thể được tính là,

Z = (x - x) / s

Z = (5 –17) / 1,90
Z = 0,44

Do đó, cách sử dụng của sinh viên thứ 3 là 0,44 lần độ lệch chuẩn so với mức sử dụng trung bình của mẫu, tức là theo bảng điểm z, 67% sinh viên sử dụng ít bút chì hơn sinh viên thứ 3.

Ví dụ # 3

Dưới đây là dữ liệu được cung cấp để tính toán Thống kê kiểm tra Z

Bạn có thể tham khảo bảng excel dưới đây để tính toán chi tiết Z Test Statistics.

Mức độ liên quan và sử dụng

Điều rất quan trọng là phải hiểu khái niệm thống kê kiểm định z vì nó thường được sử dụng bất cứ khi nào có thể tranh luận rằng liệu thống kê kiểm định có tuân theo phân phối chuẩn hay không dưới giả thuyết rỗng có liên quan. Tuy nhiên, cần lưu ý rằng phép thử z chỉ được sử dụng khi cỡ mẫu lớn hơn 30, nếu không, phép thử t sẽ được sử dụng.

seychellesartprojects.org