seychellesartprojects.org

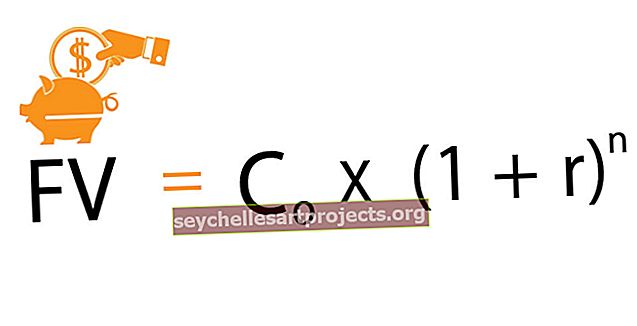
Công thức tính FV

Công thức Giá trị Tương lai (FV) là một thuật ngữ tài chính được sử dụng để tính toán giá trị của dòng tiền tại một ngày trong tương lai so với biên lai ban đầu. Mục tiêu của phương trình FV này là xác định giá trị tương lai của một khoản đầu tư tiềm năng và liệu lợi nhuận có mang lại đủ lợi nhuận so với giá trị thời gian của tiền hay không.

Công thức cho Giá trị Tương lai (FV) là:

Theo đó,

• C _{0 =} Dòng tiền tại thời điểm ban đầu (Giá trị hiện tại)
• r = Tỷ suất lợi nhuận
• n = số kỳ

Thí dụ

Bạn có thể tải xuống Mẫu Excel Giá trị Tương lai (FV) này tại đây - Mẫu Excel Giá trị Tương lai (FV)

Nếu bà Smith có $ 9,000 trong tài khoản ngân hàng của mình và bà ấy kiếm được lãi suất hàng năm là 4,5%. Với sự trợ giúp của công thức tương lai, tài khoản của cô ấy sau 15 năm sẽ là:

• FV = 9,000 * (1 + 0,045) ^ 15
• FV = 9,000 * (1,045) ^ 15
• FV = 9.000 * 1.935
• FV = $ 17.417,54

Chúng ta có thể xem xét một ví dụ khác để hiểu rõ hơn:

Bà Smith có một tài khoản khác có $ 20,000 trả lãi suất hàng năm là 11% cộng lại hàng quý. Kể từ ngày 1 tháng 1 năm 2017, các điều khoản của thỏa thuận đã được gia hạn và lãi kép được phân bổ hai lần một tháng. Bà Smith có muốn tính tổng giá trị của tài khoản vào ngày 31 tháng 12 năm 2017 không?

Trước tiên, chúng tôi cần đến số dư đầu kỳ vào ngày 1 tháng 1 năm 2017:

• PV (16 tháng 1 - 16 tháng 12) = 20.000 đô la
• Giai đoạn gộp (n) = 4
• Lãi suất hàng năm (r) = 11% chuyển thành lãi suất hàng quý là 2,75% [11% / 4]
• FV = 20.000 * (1 + 0,0275) ^ 4
• FV = 20.000 * (1,0275) ^ 4
• FV = $ 22.292,43 (Đây là số dư đầu kỳ tính đến ngày 1 tháng 1 năm 2017)

Do đó, bây giờ để tính Giá trị tương lai tại ngày 31 tháng 12 năm 2017, Giá trị hiện tại nếu $ 22.292,43.

Khoảng thời gian cộng gộp (n) bây giờ là 2 * 12 = 24 vì lãi suất kép hiện là hai lần một tháng.

Lãi suất hàng năm (r) = 11% quy đổi lãi suất hàng tháng = 11% / 12 = 0,0092 [số tiền này sẽ được chia đôi một tháng như vậy, 0,92 / 2 = 0,0046%]

• Do đó, FV = PV (1 + r) ^ n
• FV = 22.292,43 * (1 + 0,0046) ^ 24
• FV = 22.292,43 * (1.00046) ^ 24
• FV = 22.292,43 * 1,116
• FV = $ 24.888 [Giá trị của tài khoản vào ngày 31 tháng 12 năm 2017]

Sử dụng và mức độ liên quan

1. Lợi ích chính của FV là xác định xem liệu một cơ hội đầu tư có thu được đủ lợi nhuận trong tương lai hay không.
2. Khái niệm này có thể áp dụng cho các quyết định của Cá nhân và Doanh nghiệp.
3. Mục tiêu là hiểu được các yếu tố kinh tế có thể có tác động như thế nào đến thu nhập như Lạm phát, Mức sống, chi phí hoạt động / chi phí định kỳ (cần thực hiện phân tích riêng).
4. Nó cho biết dòng thanh toán dự kiến ​​sẽ nhận được trong một khoảng thời gian, ví dụ như khoản đầu tư 10 năm có thể cho biết có thể kiếm được bao nhiêu lợi nhuận mỗi năm.
5. Trong một số trường hợp nhất định, công thức cũng được sử dụng làm đầu vào cho các công thức khác. Ví dụ: niên kim dưới dạng tiền gửi định kỳ trong một tài khoản thú vị sẽ là FV của mỗi khoản tiền gửi.

Máy tính giá trị tương lai

Bạn có thể sử dụng Máy tính Giá trị Tương lai sau

C 0
r
n
Công thức Giá trị Tương lai =

Công thức Giá trị Tương lai =	C 0 X (1 + r) n =
	0 * (1 + 0) 0 = 0