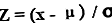seychellesartprojects.org

Công thức tính điểm Z

Điểm Z của dữ liệu thô đề cập đến điểm số được tạo ra bằng cách đo lường bao nhiêu độ lệch chuẩn trên hoặc dưới trung bình dân số là dữ liệu, giúp kiểm tra giả thuyết đang xem xét. Nói cách khác, khoảng cách của một điểm dữ liệu so với trung bình tổng thể được biểu thị dưới dạng bội số của độ lệch chuẩn.

• Điểm z thay đổi trong phạm vi từ -3 lần độ lệch chuẩn (ngoài cùng bên trái của phân phối chuẩn) đến +3 lần độ lệch chuẩn (ngoài cùng bên phải của phân phối chuẩn).
• Điểm z có giá trị trung bình là 0 và độ lệch chuẩn là 1.

Phương trình cho điểm số z của một điểm dữ liệu được tính bằng cách lấy điểm dữ liệu trừ đi trung bình tổng thể (gọi tắt là x ) và sau đó kết quả được chia cho độ lệch chuẩn tổng thể. Về mặt toán học, nó được biểu diễn dưới dạng,

Điểm Z = (x - μ) / ơ

Ở đâu

• x = Datapoint
• μ = Mean
• ơ = Độ lệch chuẩn

Tính điểm Z (Từng bước)

Phương trình cho điểm z của một điểm dữ liệu có thể được suy ra bằng cách sử dụng các bước sau:

• Bước 1: Đầu tiên, xác định giá trị trung bình của tập dữ liệu dựa trên các điểm dữ liệu hoặc quan sát được ký hiệu là x _i , trong khi tổng số điểm dữ liệu trong tập dữ liệu được ký hiệu là N.

• Bước 2: Tiếp theo, xác định độ lệch chuẩn của tổng thể trên cơ sở trung bình của tổng thể μ, các điểm dữ liệu x _i và số lượng các điểm dữ liệu trong tổng thể N.

• Bước 3: Cuối cùng, điểm số z được tính bằng cách trừ giá trị trung bình từ điểm dữ liệu và sau đó kết quả được chia cho độ lệch chuẩn như hình dưới đây.

  

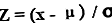
Các ví dụ

Bạn có thể tải xuống Mẫu Excel Công thức Điểm Z này tại đây - Mẫu Excel Công thức Điểm Z

Ví dụ 1

Chúng ta hãy lấy ví dụ về một lớp học có 50 học sinh đã viết bài kiểm tra khoa học tuần trước. Hôm nay là ngày kết quả và giáo viên của lớp nói rằng John đạt 93 điểm trong bài kiểm tra trong khi điểm trung bình của cả lớp là 68. Hãy xác định điểm z cho điểm kiểm tra của John nếu độ lệch chuẩn là 13.

Giải pháp:

Được,

• Điểm kiểm tra của John, x = 93
• Trung bình, μ = 68
• Độ lệch chuẩn, ơ = 13

Do đó, điểm z cho điểm kiểm tra của John có thể được tính bằng công thức trên như,

Z = (93 - 68) / 13

Điểm Z sẽ là -

Điểm Z = 1,92

Do đó, điểm Ztest của John cao hơn điểm trung bình của lớp là 1,92 độ lệch chuẩn, tức là 97,26% học sinh trong lớp (49 học sinh) đạt điểm thấp hơn John.

Ví dụ số 2

Chúng ta hãy lấy một ví dụ chi tiết khác về 30 sinh viên (vì z-test không phù hợp với ít hơn 30 điểm dữ liệu) đã xuất hiện trong một bài kiểm tra trên lớp. Xác định điểm của bài kiểm tra z cho học sinh thứ 4 dựa trên điểm của các học sinh đó trong số 100 - 55, 67, 84, 65, 59, 68, 77, 95, 88, 78, 53, 81, 73, 66 , 65, 52, 54, 83, 86, 94, 85, 72, 62, 64, 74, 82, 58, 57, 51, 91.

Giải pháp:

Được,

• x = 65,
• Học sinh thứ 4 đạt điểm = 65,
• Số điểm dữ liệu, N = 30.

Trung bình = (55 + 67 + 84 + 65 + 59 + 68 + 77 + 95 + 88 + 78 + 53 + 81 + 73 + 66 + 65 + 52 + 54 + 83 + 86 + 94 + 85 + 72 + 62 + 64 + 74 + 82 + 58 + 57 + 51 + 91) / 30

Trung bình = 71,30

Bây giờ, độ lệch chuẩn có thể được tính bằng cách sử dụng công thức như hình dưới đây,

ơ = 13,44

Do đó, điểm Z của học sinh thứ 4 có thể được tính theo công thức trên như sau:

Z = (x - x) / s

• Z = (65 –30) / 13,44
• Z = -0,47

Do đó, điểm của học sinh thứ 4 là 0,47 độ lệch chuẩn dưới điểm trung bình của lớp, có nghĩa là 31,92% của lớp (10 học sinh) đạt điểm thấp hơn học sinh thứ 4 theo bảng z-score.

Điểm Z trong Excel (với Mẫu Excel)

Bây giờ, chúng ta hãy lấy trường hợp được đề cập trong ví dụ 2 để minh họa khái niệm về điểm số z trong mẫu excel bên dưới.

Dưới đây là dữ liệu cung cấp để tính điểm Z

Bạn có thể tham khảo bảng excel cho sẵn dưới đây để tính toán chi tiết Thống kê bài thi công thức điểm Z.

Mức độ liên quan và sử dụng

Từ góc độ kiểm định giả thuyết, điểm số z là một khái niệm rất quan trọng cần hiểu vì nó được sử dụng để kiểm tra xem thống kê kiểm định có nằm trong phạm vi giá trị có thể chấp nhận được hay không. Điểm số z cũng được sử dụng để chuẩn hóa dữ liệu trước khi phân tích, tính toán xác suất của một điểm số hoặc so sánh của hai hoặc nhiều điểm dữ liệu từ các phân phối chuẩn khác nhau. Có nhiều ứng dụng đa dạng của điểm z trên các lĩnh vực nếu áp dụng đúng cách.