Công thức giá trị P | Ví dụ từng bước để tính giá trị P
Công thức Giá trị P là gì?
P là một thước đo thống kê giúp các nhà nghiên cứu xác định liệu giả thuyết của họ có đúng hay không. Nó giúp xác định tầm quan trọng của kết quả. Giả thuyết rỗng là một vị trí mặc định rằng không có mối quan hệ giữa hai hiện tượng đo được. Nó được ký hiệu là H 0. Một giả thuyết thay thế là giả thuyết mà bạn sẽ tin nếu giả thuyết vô hiệu được kết luận là không đúng sự thật. Ký hiệu của nó là H 1 hoặc H a.
Giá trị p trong excel là một số từ 0 đến 1. Có các bảng, chương trình bảng tính và phần mềm thống kê để giúp tính toán giá trị p. Mức ý nghĩa (α) là một ngưỡng được xác định trước do nhà nghiên cứu đặt ra. Nó thường là 0,05. Giá trị p rất nhỏ, nhỏ hơn mức ý nghĩa cho thấy rằng bạn bác bỏ giả thuyết vô hiệu. Giá trị P lớn hơn mức ý nghĩa chỉ ra rằng chúng ta không thể bác bỏ giả thuyết vô hiệu.
Giải thích Công thức Giá trị P
Công thức tính giá trị p có thể được rút ra bằng cách sử dụng các bước sau:
Tính giá trị P từ thống kê Z
Bước 1: Chúng ta cần tìm ra thống kê thử nghiệm z

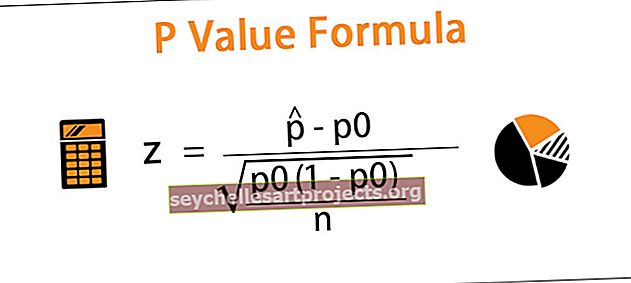
Ở đâu
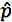 là Tỷ lệ Mẫu
là Tỷ lệ Mẫu- p0 là Tỷ lệ Dân số Giả định trong Giả thuyết Không
- n là Kích thước Mẫu
Bước 2: Chúng ta cần tìm cấp tương ứng của p từ giá trị z thu được. Với mục đích này, chúng ta cần nhìn vào bảng z.

Nguồn: www.dummies.com
Ví dụ, chúng ta hãy tìm giá trị của p tương ứng với z ≥ 2,81. Vì phân phối chuẩn là đối xứng, các giá trị âm của z bằng các giá trị dương của nó. 2,81 là tổng của 2,80 và 0,01. Nhìn vào 2,8 trong cột z và giá trị tương ứng là 0,01. Ta được p = 0,0025.
Ví dụ về Công thức Giá trị P (với Mẫu Excel)
Hãy xem một số ví dụ từ đơn giản đến nâng cao của phương trình P-Value để hiểu rõ hơn.
Bạn có thể tải xuống Mẫu Excel Công thức Giá trị P này tại đây - Mẫu Excel Công thức Giá trị P
Ví dụ 1
a) Giá trị P là 0,3015. Nếu mức ý nghĩa là 5%, hãy tìm xem chúng ta có thể bác bỏ giả thuyết vô hiệu hay không.
b) Giá trị P là 0,0129. Nếu mức ý nghĩa là 5%, hãy tìm xem chúng ta có thể bác bỏ giả thuyết vô hiệu hay không.
Giải pháp:
Sử dụng dữ liệu sau để tính giá trị P.

Giá trị P sẽ là -

a) Vì giá trị p của 0,3015 lớn hơn mức ý nghĩa 0,05 (5%) nên chúng tôi không thể bác bỏ giả thuyết vô hiệu.
b) Vì giá trị p là 0,0129 nhỏ hơn mức ý nghĩa 0,05 nên chúng tôi bác bỏ giả thuyết vô hiệu.
Ví dụ số 2
27% người dân ở Ấn Độ nói tiếng Hindi theo một nghiên cứu. Một nhà nghiên cứu tò mò liệu con số này có cao hơn ở làng của mình không. Do đó, ông đóng khung giả thuyết vô hiệu và giả thuyết thay thế. Ông kiểm tra H 0: p = 0,27. H a: p> 0,27. Ở đây, p là tỷ lệ người dân trong làng nói tiếng Hindi. Anh ấy thực hiện một cuộc khảo sát trong làng của mình để tìm ra số lượng người có thể nói tiếng Hindi. Ông phát hiện ra rằng 80 trong số 240 người được lấy mẫu có thể nói tiếng Hindi. Tìm giá trị p gần đúng cho phép thử của nhà nghiên cứu nếu chúng ta giả định rằng các điều kiện cần thiết được đáp ứng và mức ý nghĩa là 5%.
Giải pháp:
Sử dụng dữ liệu sau để tính giá trị P.

Ở đây, kích thước mẫu n = 240,
p 0 là tỷ lệ dân số Chúng ta sẽ phải tìm tỷ lệ mẫu
= 80/240
 = 0,33
= 0,33
Thống kê Z
Tính toán thống kê Z


= 0,33 - 0,27 / √ 0,27 * (1 - 0,27) / 240
Thống kê Z sẽ là -

Z = 2,093696
Giá trị P sẽ là -

Giá trị P = P (z ≥ 2,09)
Chúng ta phải xem giá trị của 2,09 là bảng z. Vì vậy, chúng ta phải xem xét -2,0 trong cột z và giá trị trong cột 0,09. Vì phân phối chuẩn là đối xứng nên diện tích bên phải của đường cong bằng với diện tích bên trái. Chúng tôi nhận được giá trị p là 0,0183.
Giá trị P = 0,0183
Vì giá trị p nhỏ hơn mức có ý nghĩa 0,05 (5%), chúng tôi bác bỏ giả thuyết vô hiệu.
Lưu ý: Trong Excel, giá trị p sắp tới là 0,0181
Ví dụ # 3
Các nghiên cứu cho thấy nam giới mua vé máy bay nhiều hơn so với nữ giới. Chúng được con đực và con cái mua theo tỷ lệ 2: 1. Nghiên cứu được thực hiện tại một sân bay cụ thể ở Ấn Độ để tìm sự phân bổ vé máy bay giữa nam và nữ. Trong tổng số 150 vé, nam có 88 vé và nữ là 62 vé. Chúng ta cần tìm hiểu xem thao tác thử nghiệm có gây ra sự thay đổi trong kết quả hay chúng ta đang quan sát một sự thay đổi ngẫu nhiên. Tính giá trị p với giả thiết mức ý nghĩa là 0,05.
Giải pháp:
Sử dụng dữ liệu sau để tính giá trị P.

Bước 1: Giá trị quan sát được là 88 đối với nam và 62 đối với nữ.
- Giá trị mong đợi cho nam = 2/3 * 150 = 100 nam
- Giá trị mong đợi cho nữ = 1/3 * 150 = 50 nữ
Bước 2: Tìm ra chi-square


= ((88-100) 2) / 100 + (62-50) 2/50
= 1,44 + 2,88
Chi-Square (X ^ 2)
Chi-Square (X ^ 2) sẽ là -

Chi-Square (X ^ 2) = 4,32
Bước 3: Tìm bậc tự do
Vì có 2 biến - nam và nữ nên n = 2
Bậc tự do = n-1 = 2-1 =
Bước 4: Từ bảng giá trị p, chúng ta nhìn vào hàng đầu tiên trong bảng vì bậc tự do là 1. Chúng ta có thể thấy rằng giá trị p nằm trong khoảng 0,025 đến 0,05. Vì giá trị p nhỏ hơn mức ý nghĩa 0,05, chúng tôi bác bỏ giả thuyết vô hiệu.
Giá trị P sẽ là -

Giá trị P = 0,037666922
Lưu ý: Excel trực tiếp cung cấp giá trị p bằng công thức:
CHITEST (phạm vi thực tế, phạm vi dự kiến)
Ví dụ # 4
Người ta biết rằng 60% những người vào các cửa hàng may mặc trong thành phố mua một thứ gì đó. Một chủ cửa hàng may mặc muốn tìm xem con số có cao hơn cho cửa hàng may mặc do anh ta làm chủ hay không. Anh ấy đã có kết quả của một cuộc nghiên cứu được thực hiện cho cửa hàng của mình. 128 trong số 200 người vào cửa hàng của anh ấy đã mua một thứ gì đó. Chủ cửa hàng biểu thị tỷ lệ những người đã vào cửa hàng quần áo của mình và mua một thứ gì đó. Giả thuyết vô hiệu được ông đưa ra là p = 0,60 và giả thuyết thay thế là p> 0,60. Tìm giá trị p của nghiên cứu với mức ý nghĩa 5%.
Giải pháp:
Sử dụng dữ liệu sau để tính giá trị P.

Ở đây, kích thước mẫu n = 200. Chúng ta sẽ phải tìm tỷ lệ mẫu
= 128/200
 = 0,64
= 0,64
Thống kê Z
Tính toán thống kê Z


= 0,64 - 0,60 / √ 0,60 * (1 - 0,60) / 200
Thống kê Z sẽ là -

Thống kê Z = 1,1547
Giá trị P = P (z ≥ 1,1547)
Hàm NORMSDIST trong Excel

NORMSDIST sẽ là -

NORMSDIST = 0,875893461
Có một hàm sẵn có để tính giá trị p từ thống kê az trong Excel. Nó được gọi là hàm NORMSDIST. Hàm NORMSDIST trong Excel tính toán Hàm phân phối tích lũy chuẩn thông thường từ một giá trị được cung cấp. Định dạng của nó là NORMSDIST (z). Vì giá trị thống kê z nằm trong ô B2 nên hàm được sử dụng là = NORMSDIST (B2).
Giá trị P sẽ là -

Giá trị P = 0,12410654
Vì chúng ta phải tìm khu vực bên phải của đường cong,
p-value = 1 - 0,875893 = 0,124107
Vì giá trị p của 0,124107 lớn hơn mức có ý nghĩa là 0,05, chúng tôi không thể bác bỏ giả thuyết vô hiệu.
Mức độ liên quan và sử dụng
P-Value có ứng dụng rộng rãi trong kiểm tra giả thuyết thống kê, đặc biệt là trong kiểm định giả thuyết rỗng. Ví dụ, một Người quản lý quỹ điều hành một quỹ tương hỗ. Ông tuyên bố rằng lợi nhuận từ một chương trình cụ thể của quỹ tương hỗ tương đương với Nifty, là chỉ số thị trường chứng khoán chuẩn. Ông sẽ đóng khung giả thuyết vô hiệu rằng lợi nhuận của chương trình quỹ tương hỗ tương đương với lợi nhuận của Nifty. Giả thuyết thay thế sẽ là lợi nhuận của Scheme và lợi nhuận Nifty không tương đương nhau. Sau đó anh ta sẽ tính toán giá trị p.

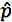 là Tỷ lệ Mẫu
là Tỷ lệ Mẫu