seychellesartprojects.org

Công thức xác định cỡ mẫu của dân số

Công thức Cỡ mẫu giúp tính toán hoặc xác định cỡ mẫu tối thiểu cần thiết để biết tỷ lệ dân số thích hợp hoặc chính xác cùng với mức độ tin cậy và biên độ sai số.

Thuật ngữ “mẫu” đề cập đến phần dân số cho phép chúng ta rút ra các suy luận về dân số và do đó, điều quan trọng là kích thước mẫu phải đủ để có thể đưa ra các suy luận có ý nghĩa. Nói cách khác, đó là kích thước tối thiểu cần thiết để ước tính tỷ lệ dân số thực với biên độ sai số và mức độ tin cậy cần thiết. Do đó, việc xác định cỡ mẫu thích hợp là một trong những vấn đề thường xuyên trong phân tích thống kê. Phương trình của nó có thể được rút ra bằng cách sử dụng kích thước dân số, giá trị tới hạn của phân phối chuẩn, tỷ lệ mẫu và biên sai số.

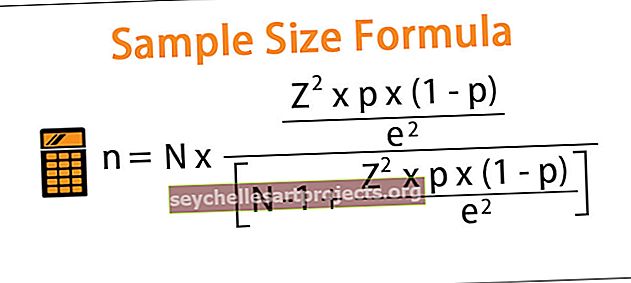
Ở đâu,

• N = Quy mô dân số,
• Z = Giá trị tới hạn của phân phối chuẩn ở mức độ tin cậy cần thiết,
• p = Tỷ lệ mẫu,
• e = Biên độ lỗi

Làm thế nào để tính toán kích thước mẫu? (Từng bước một)

• Bước 1: Trước tiên, xác định quy mô dân số là tổng số thực thể riêng biệt trong quần thể của bạn và nó được ký hiệu là N. [Lưu ý: Trong trường hợp quy mô dân số rất lớn nhưng không biết được con số chính xác thì sử dụng 100.000 bởi vì kích thước mẫu không thay đổi nhiều đối với các quần thể lớn hơn thế.]
• Bước 2: Tiếp theo, xác định giá trị tới hạn của phân phối chuẩn ở mức độ tin cậy cần thiết. Ví dụ, giá trị tới hạn ở độ tin cậy 95% là 1,96.
• Bước 3: Tiếp theo, xác định tỷ lệ mẫu có thể được sử dụng từ các kết quả điều tra trước đó hoặc được thu thập bằng cách thực hiện một cuộc điều tra thí điểm nhỏ. [Lưu ý: nếu không chắc, người ta luôn có thể sử dụng 0,5 như một cách tiếp cận thận trọng và nó sẽ cung cấp kích thước mẫu lớn nhất có thể.]
• Bước 4: Tiếp theo, xác định biên độ sai số là phạm vi mà dân số thực dự kiến ​​sẽ nói dối . [Lưu ý: Biên độ sai số càng nhỏ thì độ chính xác càng cao và do đó có câu trả lời chính xác.]
• Bước 5: Cuối cùng, phương trình kích thước mẫu có thể được rút ra bằng cách sử dụng quy mô dân số (bước 1), giá trị tới hạn của phân phối chuẩn ở mức độ tin cậy cần thiết (bước 2), tỷ lệ mẫu (bước 3) và biên sai số (bước 4) như hình dưới đây.

Các ví dụ

Bạn có thể tải xuống Mẫu Excel Công thức Kích thước Mẫu này tại đây - Mẫu Excel Công thức Kích thước Mẫu

Ví dụ 1

Chúng ta hãy lấy ví dụ về một nhà bán lẻ muốn biết có bao nhiêu khách hàng của họ đã mua một mặt hàng từ họ sau khi xem trang web của họ vào một ngày nhất định. Giả sử rằng trang web của họ có trung bình 10.000 lượt xem mỗi ngày, hãy xác định quy mô mẫu của khách hàng mà họ phải theo dõi ở mức độ tin cậy 95% với sai số 5% nếu:

• Họ không chắc chắn về tỷ lệ chuyển đổi hiện tại.
• Họ biết từ các cuộc khảo sát trước đây rằng tỷ lệ chuyển đổi là 5%.

Được,

• Quy mô dân số, N = 10.000
• Giá trị tới hạn ở độ tin cậy 95%, Z = 1,96
•  Biên độ sai số, e = 5% hoặc 0,05

1 - Vì tỷ lệ chuyển đổi hiện tại là không xác định, chúng ta hãy giả sử p = 0,5

Do đó, kích thước mẫu có thể được tính bằng công thức như,

= (10.000 * (1,96 2) * 0,5 * (1-0,5) / (0,05 2) / (10000 - 1 + ((1,96 2) * 0,5 * (1-0,5) / (0,05 2))))

Do đó, 370 khách hàng sẽ đủ để đưa ra suy luận có ý nghĩa.

2 - Tỷ lệ chuyển đổi hiện tại là p = 5% hoặc 0,05

Do đó, kích thước mẫu có thể được tính theo công thức trên là,

= (10.000 * (1,96 2) * 0,05 * (1-0,05) / (0,05 2) / (10000 - 1 + ((1,96 2) * 0,05 * (1-0,05) / (0,05 2))))

Do đó, quy mô 72 khách hàng sẽ là đủ để đưa ra suy luận có ý nghĩa trong trường hợp này.

Ví dụ số 2

Chúng ta hãy lấy ví dụ trên và trong trường hợp này, chúng ta hãy giả định rằng quy mô dân số, tức là lượt xem trang web hàng ngày, là từ 100.000 đến 120.000, nhưng khi đó giá trị chính xác không được biết đến. Các giá trị còn lại đều giống nhau cùng với tỷ lệ chuyển đổi là 5%. Tính cỡ mẫu cho cả 100.000 và 120.000.

Được,

• Tỷ lệ mẫu, p = 0,05
• Giá trị tới hạn ở độ tin cậy 95%, Z = 1,96
•  Biên độ sai số, e = 0,05

Do đó, cỡ mẫu cho N = 100.000 có thể được tính là,

= (100000 * (1,96 2) * 0,05 * (1-0,05) / (0,05 2) / (100000 - 1 + ((1,96 2) * 0,05 * (1-0,05) / (0,05 2))))

Do đó, cỡ mẫu cho N = 120.000 có thể được tính là,

= (120000 * (1,96 2) * 0,05 * (1-0,05) / (0,05 2) / (120000 - 1 + ((1,96 2) * 0,05 * (1-0,05) / (0,05 2))))

Do đó, người ta chứng minh rằng khi quy mô dân số tăng lên rất lớn, nó trở nên không phù hợp trong việc tính toán kích thước mẫu.

Mức độ liên quan và sử dụng

Việc tính toán cỡ mẫu rất quan trọng để hiểu được khái niệm cỡ mẫu thích hợp vì nó được sử dụng để đảm bảo tính hợp lệ của các kết quả nghiên cứu. Trong trường hợp quá nhỏ, nó sẽ không mang lại kết quả hợp lệ, trong khi một mẫu quá lớn có thể gây lãng phí cả tiền bạc và thời gian. Về mặt thống kê, cỡ mẫu quan trọng chủ yếu được sử dụng cho các cuộc khảo sát nghiên cứu thị trường, khảo sát chăm sóc sức khỏe và khảo sát giáo dục.