seychellesartprojects.org

R Bình phương (R2) trong Hồi quy là gì?

R-bình phương (R2) là một thước đo thống kê quan trọng, là một mô hình hồi quy biểu thị tỷ lệ của sự khác biệt hoặc phương sai về mặt thống kê cho một biến phụ thuộc có thể được giải thích bằng một biến hoặc các biến độc lập. Tóm lại, nó xác định mức độ phù hợp của dữ liệu với mô hình hồi quy.

Công thức bình phương R

Để tính toán R bình phương, bạn cần xác định Hệ số tương quan và sau đó bạn cần bình phương kết quả.

R Công thức bình phương = r2

Trong đó r, hệ số tương quan có thể được tính theo bên dưới:

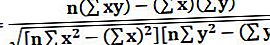
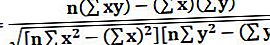
Ở đâu,

• r = Hệ số tương quan
• n = số trong tập dữ liệu đã cho
• x = biến đầu tiên trong ngữ cảnh
• y = biến thứ hai

Giải trình

Nếu có bất kỳ mối quan hệ hoặc mối tương quan nào có thể là tuyến tính hoặc không tuyến tính giữa hai biến đó thì nó sẽ cho biết nếu có sự thay đổi trong giá trị của biến độc lập, thì biến phụ thuộc khác có thể sẽ thay đổi về giá trị, nói tuyến tính hoặc không tuyến tính.

Phần tử số của công thức tiến hành kiểm tra xem chúng có chuyển động cùng nhau và loại bỏ các chuyển động riêng lẻ của chúng và sức mạnh tương đối của cả hai chuyển động cùng nhau hay không và phần mẫu số của công thức sẽ chia tỷ lệ tử số bằng cách lấy căn bậc hai của tích các chênh lệch của các biến từ các biến bình phương của chúng. Và khi bạn bình phương kết quả này, chúng ta nhận được R bình phương không là gì khác ngoài hệ số xác định.

Các ví dụ

Bạn có thể tải xuống Mẫu Excel Công thức Bình phương R này tại đây - Mẫu Excel Công thức Bình phương R

Ví dụ 1

Hãy xem xét hai biến x và y sau đây, bạn bắt buộc phải tính R Bình phương trong Hồi quy.

Giải pháp:

Sử dụng công thức nêu trên, trước tiên chúng ta cần tính toán hệ số tương quan.

Ta có tất cả các giá trị trong bảng trên với n = 4.

Bây giờ chúng ta hãy nhập các giá trị trong công thức để có được hình.

r = (4 * 26.046,25) - (265,18 * 326,89) / √ [(4 * 21,274,94) - (326,89) 2] * [(4 * 31,901,89) - (326,89) 2]

r = 17.501,06 / 17.512,88

Hệ số tương quan sẽ-

r = 0,99932480

Vì vậy, cách tính sẽ như sau,

r2 = (0,99932480) 2

Công thức bình phương R trong hồi quy

r2 = 0,998650052

Ví dụ số 2

Ấn Độ, một quốc gia đang phát triển muốn tiến hành một cuộc phân tích độc lập liệu những thay đổi về giá dầu thô có ảnh hưởng đến giá trị đồng rupee của nước này hay không. Sau đây là lịch sử của giá dầu thô Brent và định giá đồng Rupee so với đồng đô la, mức trung bình phổ biến trong những năm dưới đây.

RBI, ngân hàng trung ương của Ấn Độ đã tiếp cận bạn để cung cấp một bài thuyết trình về vấn đề tương tự trong cuộc họp tiếp theo. Xác định xem biến động của dầu thô có ảnh hưởng đến chuyển động của Rupee trên một đô la hay không?

Giải pháp:

Sử dụng công thức cho mối tương quan ở trên, chúng ta có thể tính toán hệ số tương quan trước. Coi giá dầu thô trung bình là một biến số nói là x và coi Rupee trên mỗi đô la là một biến số khác là y.

Ta có tất cả các giá trị trong bảng trên với n = 6.

Bây giờ chúng ta hãy nhập các giá trị trong công thức để có được hình.

r = (6 * 23592,83) - (356,70 * 398,59) / √ [(6 * 22829,36) - (356,70) 2] * [(6 * 26529,38) - (398,59) 2]

r = -620,06 / 1.715,95

Hệ số tương quan sẽ-

r = -0,3614

Vì vậy, cách tính sẽ như sau,

r2 = (-0,3614) 2

Công thức bình phương R trong hồi quy

r2 = 0,1306

Phân tích: Có vẻ như có một mối quan hệ nhỏ giữa thay đổi giá dầu thô và thay đổi giá đồng rupee Ấn Độ. Khi giá dầu thô tăng, đồng rupee Ấn Độ thay đổi cũng ảnh hưởng. Nhưng vì R bình phương chỉ là 13% nên những thay đổi trong giá dầu thô giải thích rất ít về những thay đổi của đồng rupee Ấn Độ và đồng rupee Ấn Độ có thể thay đổi trong các biến số khác cũng như cần được tính đến.

Ví dụ # 3

Phòng thí nghiệm XYZ đang tiến hành nghiên cứu về chiều cao và cân nặng và muốn biết liệu có bất kỳ loại mối quan hệ nào giữa các biến số này hay không. Sau khi thu thập mẫu gồm 5000 người cho mọi danh mục và đưa ra trọng lượng trung bình và chiều cao trung bình trong nhóm cụ thể đó.

Dưới đây là các chi tiết mà họ đã thu thập được.

Bạn được yêu cầu tính R Bình phương và kết luận xem mô hình này có giải thích được các phương sai về chiều cao có ảnh hưởng đến phương sai về cân nặng hay không.

Giải pháp:

Sử dụng công thức cho mối tương quan ở trên, chúng ta có thể tính toán hệ số tương quan trước. Coi chiều cao là một biến là x và coi cân nặng là một biến khác là y.

Ta có tất cả các giá trị trong bảng trên với n = 6.

Bây giờ chúng ta hãy nhập các giá trị trong công thức để có được hình.

r = (7 * 74.058,67) - (1031 * 496,44) / √ [(7 * 153595 - (1031) 2] * [(7 * 35793,59) - (496,44) 2]

r = 6.581,05 / 7.075,77

Hệ số tương quan sẽ-

Hệ số tương quan (r) = 0,930

Vì vậy, cách tính sẽ như sau,

r2 = 0,865

Phân tích: Mối tương quan là cùng chiều, và có vẻ như có một số mối quan hệ giữa chiều cao và cân nặng khi chiều cao tăng lên thì cân nặng của một người cũng dường như tăng lên. Trong khi R2 gợi ý rằng 86% thay đổi thuộc tính chiều cao đối với thay đổi cân nặng và 14% là không giải thích được.

Mức độ liên quan và sử dụng

Mức độ liên quan của R bình phương trong hồi quy là khả năng của nó để tìm xác suất của các sự kiện trong tương lai xảy ra trong các kết quả dự đoán đã cho hoặc các kết quả. Nếu nhiều mẫu hơn được thêm vào mô hình, thì hệ số sẽ hiển thị khả năng xảy ra hoặc xác suất của một điểm mới hoặc tập dữ liệu mới rơi vào dòng. Ngay cả khi cả hai biến có mối liên hệ chặt chẽ, việc xác định không chứng minh được quan hệ nhân quả.

Một số không gian mà bình phương R chủ yếu được sử dụng là để theo dõi hoạt động của quỹ tương hỗ, để theo dõi rủi ro trong quỹ đầu cơ, để xác định mức độ di chuyển của cổ phiếu với thị trường, trong đó R2 sẽ gợi ý mức độ biến động của cổ phiếu có thể được giải thích bởi các chuyển động trên thị trường.